Details that Make a Difference

George E. Smith may be the best kept secret in academia.

The words aren’t mine: they belong to Daniel Dennett.* He said them yesterday at On the Question of Evidence, a conference Tufts University hosted to celebrate George’s life and work. George sat in the second row during the day’s presentations. I watched him listen attentively, every once and a while bowing his head the way he does when he gets emotional, humbly displacing praise to another giant upon whose shoulders he claims to have stood. I. Bernard Cohen, Ken Wilson, Curtis Wilson, Tom Whiteside (I remember George’s anecdote about meeting Whiteside in a bookstore and saying he genuflected before his brilliant scholarship on Newtonian mathematics). He unabashedly had the first word after every talk, most of the time articulating an anecdote (anyone who knows George knows that he likes to tell stories) about how someone else taught him an idea or taking the opportunity to articulate some crisp, crucial maxim in philosophy of science. Perhaps my favourite part of the entire day was listening to him interrupt Dan’s story about how they jointly founded the computer science program at Tufts, back in the days of Minsky and Good ol’ fashioned AI**, George stepping in to provide additional details about their random colour pixel generation program (random until the output looked a little too much like plaid), recollecting dates and details with ludicrous precision, as is his capability and wont.

Almost every conference attendee had at least one thing in common: we’d taken George’s Newton seminar, unique in its kind, one of the most complete, erudite, stimulating academic experiences in the world today. Some conference attendees, like Eric Schliesser and Bill Bradley, took the seminar back in its infancy in the 80s and early 90s. I took it with Kant scholar Michael Friedman at Stanford in 2009. Each year George builds on the curriculum, collaborating with students on some open research question, only to incorporate new learnings into next year’s (or some future year’s) curriculum. Perhaps the hallmark of a truly significant thinker is that her work is as rich and complex as the natural world, containing second-order ideas like second-order phenomena, phenomena that no one observes-or even can observe!-the first time they look. Details masked behind more dominant regularities, but that, in time and through the gradual and patience process of measurement, observation, and research, become visible through the mediation of theory. Theories as anchors to see the invisible.

This recursive process of knowledge and growth isn’t unique to George’s teaching. It characterizes his seminal contribution to the philosophy of science.

Many of the conference speakers drew from George’s stunning 2014 article Closing the Loop. The article is the culmination of 20 years of work studying how Newton changed standards for high-quality evidence. We often assume that Newton’s method is hypothetical-deductive, where the reasoning structure is to formulate a hypothesis that could be falsified by a test on observable data, and collect observations to either falsify (if observations disagree with what the hypothesis predicts) or corroborate (if observations agree) a theory.*** George thinks that Newton is up to something different. He cites Newton’s “Copernicum scholium,” where Newton states that, given the complexities of forces that determine planetary motion, considering “simultaneously all these causes of motion and [defining] these motions by exact laws admitting of easy calculation exceeds…the force of any human mind.” George writes:

The complexity of true motions was always going to leave room for competing theories if only because the true motions were always going to be beyond precise description, and hence there could always be multiple theories agreeing with observation to any given level of approximation. On my reading, the Principia is one sustained response to this evidence problem.

George goes on to argue that Newtonian idealizations, the simplified, geometric theories that predict how a particular system of bodies would behave under specifiable circumstances, aren’t theories to align directly with observations, but thinking tools, counterfactuals that predict how the world would behave if it were only governed by a few forces (e.g., a system only subject to gravity versus a system subject to gravity and magnetism). Newton expects that observations won’t fit predictions, because he knows the world is more complex than mathematical models can describe. Instead, discrepancies become a source of high-quality evidence to both corroborate a theory and render hypotheses ever more precise and encompassing as we incorporate in new details about the world. If Newton can isolate how a system would behave under the force of gravity, the question becomes, what, if any, further forces are at work? According to George, then, Newton didn’t propose a static method for falsifying hypotheses with observations and data. He proposed a dynamic research strategy that could encompass an ongoing program of navigating the gulf between idealizations and observations. Importantly, as Michael Friedman showed in his talk, theories can be the necessary condition for certain types of measurement: there is a difference between plotting data points indicating the position of Jupiter at two points in time and measuring Jupiter’s acceleration in its orbit. The second is theory-mediated measurement, where the theory relating mass to acceleration via the force of gravity makes it possible to measure mass from acceleration. Also importantly, because discrepancies between theory and observations don’t direct falsify a hypothesis, the Newtonian scientific paradigm was more resilient, requiring a different type of discrepancy to pave the way to General Relativity (while I get the gist of why Einstein required space-time curvature to explain the precession of Mercury’s orbit, I must admit I don’t yet understand it as deeply as I’d like).****

While George is widely recognized as one of the world’s foremost experts in Isaac Newton, his talents and interests are wide-ranging. Alongside his career as a philosopher, he has a second, fully-developed career (not just a hobby) as a jet engine engineer focused on failure analysis. He has a keen sensibility for literature: he introduced me to Elena Ferrante, whose Neapolitan novels I have sense devoured. He knows his way around modern art, having dated artist Eva Hesse during his undergraduate years at Yale. He treats his wife India, who is herself incredible, with love and respect. He takes pride in having coached basketball to underprivileged students on Boston’s south side. The list literally goes on and on.

The commentary that touched me deepest came from Tufts Dean of Academic Affairs Nancy Bauer. Nancy commented on the fact that she wouldn’t be where she is today if it weren’t for George, that he believed there was a place for feminist philosophy in the academy before other departments caught on. She also commented on what is perhaps George’s most important skill: his ability to at once challenge students to rise to just beyond the limits of their potential and to imbue them with the confidence they need to succeed.

This is not meaningful to me in the abstract. It is concrete and personal.

I took George’s course during the spring trimester of my second year in graduate school. I was intimidated: my graduate degree is in comparative literature, and while I had majored in mathematics as an undergrad, I was unwaveringly insecure about my abilities to reason precisely. Some literature students are comfortable in their skin; they live and breath words, images, tropes, analogies. I teetered in a no man’s land between math, philosophy, history, literature, gorging with curiosity and encyclopedic drive but never disciplined enough to do one thing with excellence. The first (or second? George would know…) day of class, I approached George and told him I was worried about taking the course as a non-philosopher. I was definitely concerned few times trying to muscle my way through the logic of Newton’s proofs in the Principia (it was heartening to learn that John Locke barely understood it). But George asked me about my background and, learning I’d studied math, smiled in a way that couldn’t but give me confidence. He helped me define a topic for my final paper focused on the history of math, evaluating the concept of what Newton calls “first and last ratios”, akin to but not quite limits, in the Principia. He was proud of my paper. I was proud of my paper. But what matters is not the scholarship, it’s what I learned in the process.

George taught me how to overcome my insecurities and find a place of strength to do great work. He taught me how to love my future students, my future colleagues, how to pay close attention to their strengths, interests, weaknesses, and to shape experiences that can push them to be their best while imbuing them with the confidence they need to succeed. I carry the experience I had in George’s course with me every day to work. He taught me what it means to act with integrity as a mentor, colleague, and teacher.

I’ll close with an excerpt from an email George sent me September 29, 2017. I’d sent him a copy of Melville’s The Confidence Man to thank him for being on my podcast. Closing his thank you note, he wrote:

“I was pleased with your comment in the note attached to the gift about continuing influence. You had already, however, given me one of the more special gifts I have received in the last couple of years, namely the name of your site. I find nothing in life more gratifying than to see that someone learned something in one of my classes that they have continued to find special.”

Quam proxime, “most nearly to the highest degree possible,” occurs 139 times in the Principia. George became obsessed with what it means for grasping the place for approximation in Newtonian science. I co-opted it to refer to my own quest to achieve the delicate, precious balance between precision and soul, to guide me in my quest for meaning. How grateful I am that George is part of my process, always continuing, always growing, as we migrate the beautiful complexities of our world.

*George and Dan were my second guests on the In Context podcast, during which we discussed the relationship between data and evidence.

**Over lunch, “uncle Dan” (again, his words, not mine) predicted that the current generation of deep learning researchers would likely take a bottoms up, trial and error approach to inferring the same structured, taxonomical web of knowledge the GOFAI research community tried to define top down back in the 1950s-80s, of course will a bit more lubrication than the brittle systems of yore. This shouldn’t surprise anyone familiar with Dan’s work, as he often, as in From Bacteria to Bach and Back, writes about systems that appear to exhibit the principles of top-down intelligent design without ever having had an intentional intelligent designer. For example, life and minds.

***I won’t go into the nuances of scientific reasoning in this post, so won’t talk about processes to use data to select amidst competing hypotheses.

****I asked Bill Harper a question about the difference between Bayesian uncertainty and the delta between prediction, likelihood, and data, and the uncertainty and approximations George bakes into the Newtonian research paradigm. I’m looking to better understand different types of inference.

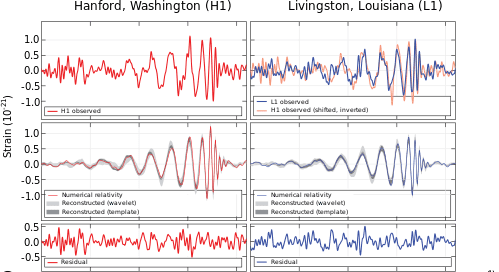
The featured image shows the overlap between the observed and predicted values of gravitational waves, observed by two Laser Interferometer Gravitational-Wave Observatories (LIGOs) in Washington and Louisiana on September 14, 2015. Allan Franklin, one of the conference speakers, showed this image and pointed out he found the visual proof of the overlap between prediction and observation more compelling than the 5-sigma effect in the data (that’s an interesting epistemological question about evidence!). He also commented how wonderful it must have been to be in the room with the LIGO researches when the event occurred. To learn more, I highly recommend Janna Levin’s Black Hole Blues and Other Sounds from Outer Space.