Imagine it’s December 26. You’re right smack in the midst of your Boxing Day hangover, feeling bloated and headachy and emotionally off from the holiday season’s interminable festivities. You forced yourself to eat Aunt Mary’s insipid green bean casserole out of politeness and put one too many shots of dark rum in your eggnog. The chastising power of the prefrontal cortex superego is in full swing: you start pondering New Year’s Resolutions.
Lose weight! Don’t drink red wine for a year! Stop eating gluten, dairy, sugar, processed foods, high-fructose corn syrup-just stop eating everything except kale, kefir, and kimchi! Meditate daily! Go be a free spirit in Kerala! Take up kickboxing! Drink kombucha and vinegar! Eat only purple foods!
Right. Check.
(5:30 pm comes along. Dad’s offering single malt scotch. Sure, sure, just a bit…neat, please…)**
We’re all familiar with how hard it is to set and stick to resolutions. That’s because our brains have little instant gratification monkeys flitting around on dopamine highs in constant guerrilla warfare against the Rational Decision Maker in the prefrontal cortex (Tim Urban’s TEDtalk on procrastination is a complete joy). It’s no use beating ourselves up over a physiological fact. The error of Western culture, inherited from Catholicism, is to stigmatize physiology as guilt, transubstantiating chemical processes into vehicles of self deprecation with the same miraculous power used to transform just-about-cardboard wafers into the living body of Christ. Eastern mindsets, like those proselytized by Buddha, are much more empowering and pragmatic: if we understand our thoughts and emotions to be senses like sight, hearing, touch, taste, smell, we can then dissociate self from thoughts. Our feelings become nothing but indices of a situation, organs to sense a misalignment between our values-etched into our brains as a set of habitual synaptic pathways-and the present situation around us. We can watch them come in, let them sit there and fester, and let them gradually fade before we do something we regret. Like waiting out the internal agony until the baby in front of you in 27G on your overseas flight to Sydney stops crying.
Resolutions are so hard to keep because we frame them the wrong way. We often set big goals, things like, “in 2017 I’ll lose 30 pounds” or “in 2017 I’ll write a book.” But a little tweak to the framework can promote radically higher chances for success. We have to transform a long-term, big, hard-to-achieve goal into a short-term, tiny, easy-to-achieve action that is correlated with that big goal. So “lose weight” becomes “eat an egg rather than cereal for breakfast.” “Write a book” becomes “sit down and write for 30-minutes each day.” “Master Mandarin Chinese” becomes “practice your characters for 15 minutes after you get home from work.” The big, scary, hard-to-achieve goal that plagues our consciousness becomes a small, friendly, easy-to-achieve action that provides us with a little burst of accomplishment and satisfaction. One day we wake up and notice we’ve transformed.
It’s doubtful that the art of finding a proxy for something that is hard to achieve or know is the secret of the universe. But it may well be the secret to adapting the universe to our measly human capabilities, both at the individual (transform me!) and collective (transform my business!) level. And the power extends beyond self-help: it’s present in the history of mathematics, contemporary machine learning, and contemporary marketing techniques known as growth hacking.
Ut unum ad unum, sic omnia ad omnia: Archimedes, Cavalieri, and Calculus
Many people are scared of math. Symbols are scary: they’re a type of language and it takes time and effort to learn what they mean. But most of the time people struggle with math because they were badly taught. There’s no clearer example of this than calculus, where kids memorize equations that something is so instead of conceptually grasping why something is so.
The core technique behind calculus-and I admit this just scratches the surface-is to reduce something that’s hard to know down to something that’s easy to know. Slope is something we learn in grade school: change in y divided by change in x, how steep a line is. Taking the derivative is doing this same process but on a twisting, turning, meandering curve rather than just a line. This becomes hard because we add another dimension to the problem: with a line, the slope is the same no matter what x we put in; with a curve, the slope changes with our x input value, like a mountain range undulating from mesa to vertical extreme cliff. What we do in differential calculus is find a way to make a line serve as a proxy for a curve, to turn something we don’t know how to do and into something know how to do. So we take magnifying glasses with ever increasing potency and zoom in until our topsy-turvy meandering curve becomes nothing but a straight line; we find the slope; and then we sum up those little slopes all the way across our curve. The big conceptual breakthrough Newton and Leibniz made in the 17th century was to turn this proxy process into something continuous and infinite: to cross a conceptual chasm between a very, very small number and a number so small that it was effectively zero. Substituting close-enough-for-government-work-zero with honest-to-goodness-zero did not go without strong criticism from the likes of George Berkeley, a prominent philosopher of the period who argued that it’s impossible for us to say anything about the real world because we can only know how our minds filter the real world. But its pragmatic power to articulate the mechanics of the celestial motions overcame such conceptual trifles.***
This type of thinking, however, did not start in the 17th century. Greek mathematicians like Archimedes (famous for screaming Eureka! (I’ve found it!) and running around naked like a madman when he noticed that water levels in the bathtub rose proportionately to his body mass) used its predecessor, the method of exhaustion, to find the area of a shape like a circle or a blob by inscribing it within a series of easier-to-measure shapes like polygons or squares to get an approximation of the area by proxy to the polygon.
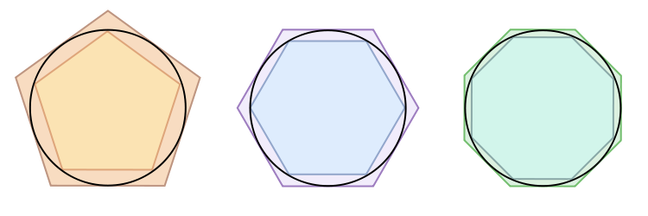
It’s challenging for us today to reimagine what Greek geometry was like because we’re steeped in a post-Cartesian mindset, where there’s an equivalence between algebraic expressions and geometric shapes. The Greeks thought about shapes as shapes. The math was tactical, physical, tangible. This mindset leads to interesting work in the Renaissance like Bonaventura’s Cavalieri’s method of indivisibles, which showed that the areas of two shapes were equivalent (often a hard thing to show) by cutting the shapes into parts and showing that each of the parts were equivalent (an easier thing to show). He turns the problem of finding equivalence into an analogy, ut unum ad unum, sic omnia ad omnia-as the one is to the one, so all are to all-substituting the part for the whole to turn this in a tractable problem. His worked paved the way for what would eventually become the calculus.****
Supervised Machine Learning for Dummies
My dear friend Moises Goldszmidt, currently Principal Research Scientist at Apple and a badass Jazz musician, once helped me understand that supervised machine learning is quite similar.
Again, at an admittedly simplified level, machine learning can be divided into two camps. Unsupervised machine learning is using computers to find patterns in data and sort different data into clusters. When most people hear they world machine learning, they think about unsupervised learning: computers automagically finding patterns, “actionable insights,” in data that would evade detection of measly human minds. In fact, unsupervised learning is an area of research in the upper echelons of the machine learning community. It can be valuable for exploratory data analysis, but only infrequently powers the products that are making news headlines. The real hero of the present day is supervised learning.
I like to think about supervised learning as follows:

Let’s take a simple example. We’re moving, and want to know how much to put our house on the market for. We’re not real estate brokers, so we’re not great at measuring prices. But we do have a tape measure, so we are great at measuring the square footage of our house. Let’s say we go look through a few years of real estate records, and find a bunch of data points about how much houses go for and what their square footage is. We also have data about location, amenities like an in-house washer and dryer, and whether the house has a big back yard. But we notice a lot of variation in prices for houses with different sized back yards, but pretty consistent correlations between square footage and price. Eureka! we say, and run around the neighbourhood naked horrifying our neighbours! We can just plot the various data points of square footage : price, measure our square footage (we do have our handy tape measure), and then put that into a function that outputs a reasonable price!
This technique is called linear regression. And it’s the basis for many data science and machine learning techniques.
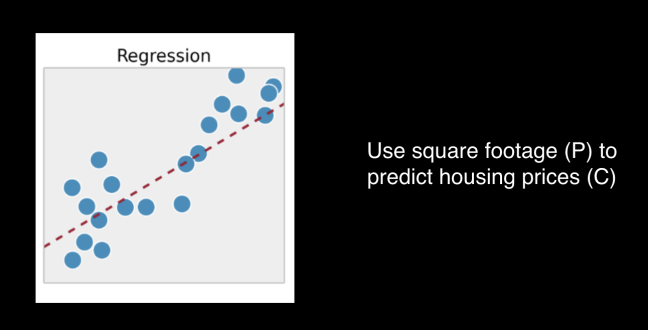
The big breakthroughs in deep learning over the past couple of years (note, these algorithms existed for a while, but they are now working thanks to more plentiful and cheaper data, faster hardware, and some very smart algorithmic tweaks) are extensions of this core principle, but they add the following two capabilities (which are significant):
- Instead of humans hand selecting a few simple features (like square footage or having a washer/dryer), computers transform rich data into a vector of numbers and find all sorts of features that might evade our measly human minds
- Instead of only being able to model phenomena using simple linear lines, deep learning neural networks can model phenomena using topsy-turvy-twisty functions, which means they can capture richer phenomena like the environment around a self-driving car
At its root, however, even deep learning is about using mathematics to identify a good proxy to represent a more complex phenomenon. What’s interesting is that this teaches us something about the representational power of language: we barter in proxies at every moment of every day, crystallizing the complexities of the world into little tokens, words, that we use to exchange our experience with others. These tokens mingle and merge to create new tokens, new levels of abstraction, adding from from the dust from which we’ve come and to which we will return. Our castles in the sky. The quixotic figures of our imagination. The characters we fall in love with in books, not giving a dam that they never existed and never will. And yet, children learn that dogs are dogs and cats are cats after only seeing a few examples; computers, at least today, need 50,000 pictures of dogs to identify the right combinations of features that serve as a decent proxy for the real thing. Reducing that quantity is an active area of research.
Growth Hacking: 10 Friends in 14 Days
I’ve spent the last month in my new role at integrate.ai talking with CEOs and innovation leaders at large B2C businesses across North America. We’re in that miraculously fun, pre product-market fit phase of startup life where we have to make sure we are building a product that will actually solve a real, impactful, valuable business problem. The possibilities are broad and we’re managing more unknown unknowns than found in a Donald Rumsfeld speech (hat tip to Keith Palumbo of Cylance for the phrase). But we’re starting to see a pattern:
- B2C businesses have traditionally focused on products, not customers. Analytics have been geared towards counting how many widgets were sold. They can track how something moves across a supply chain, but cannot track who their customers are, where they show up, and when. They can no longer compete on just product. They want to become customer centric.
- All businesses are sustained by having great customers. Great means having loyalty and alignment with brand and having a high life-time value. They buy, they buy more, they don’t stop buying, and there’s a positive association when they refer a brand to others, particularly others who behave like them.
- Wanting great customers is not a good technical analytics problem. It’s too fuzzy. So we have to find a way to transform a big objective into a small proxy, and focus energy and efforts on doing stuff in that small proxy window. Not losing weight, but eating an egg instead of pancakes for breakfast every morning.
Silicon Valley giants like Facebook call this type of thinking growth hacking: finding some local action you can optimize for that is a leading indicator of a long-term, larger strategic goal. The classic example from Facebook (which some rumour to be apocryphal, but it’s awesome as an example) was when the growth team realized that the best way to achieve their large, hard-to-achieve metric of having as many daily active users as possible was to reduce it to a smaller, easy-to-achieve metric of getting new users up to 10 friends in their first 14 days. 10 was the threshold for people’s ability to appreciate the social value of the site, a quantity of likes sufficient to drive dopamine hits that keep users coming back to the site.***** These techniques are rampant across Silicon Valley, with Netflix optimizing site layout and communications when new users join given correlations with potential churn rates down the line and Eventbrite making small product tweaks to help users understand they can use to tool to organize as well as attend events. The real power they unlock is similar to that of compound interest in finance: a small investment in your twenties can lead to massive returns after retirement.
Our goal at integrate.ai is to bring this thinking into traditional enterprises via a SaaS platform, not a consulting services solution. And to make that happen, we’re also scouting small, local wins that we believe will be proxies for our long-term success.
Conclusion
The spirit of this post is somewhat similar to a previous post about artifice as realism. There, I surveyed examples of situations where artifice leads to a deeper appreciation of some real phenomenon, like when Mendel created artificial constraints to illuminate the underlying laws of genetics. Proxies aren’t artifice, they’re parts that substitute for wholes, but enable us to understand (and manipulate) wholes in ways that would otherwise be impossible. Doorways into potential. A shift in how we view problems that makes them tractable for us, and can lead to absolutely transformative results. This takes humility. The humility of analysis. The practice of accepting the unreasonable effectiveness of the simple.
*Shout out to the amazing Andrej Karpathy, who authored The Unreasonable Effectiveness of Recurrent Neural Networks and Deep Reinforcement Learning: Pong from Pixels, two of the best blogs about AI available.
**There’s no dearth of self-help books about resolutions and self-transformation, but most of them are too cloying to be palatable. Nudge by Cass Sunstein and Richard Thaler is a rational exception.
***The philosopher Thomas Hobbes was very resistant to some of the formal developments in 17th-century mathematics. He insisted that we be able to visualize geometric objects in our minds. He was relegated to the dustbins of mathematical history, but did cleverly apply Euclidean logic to the Leviathan.
****Leibniz and Newton were rivals in discovering the calculus. One of my favourite anecdotes (potentially apocryphal?) about the two geniuses is that they communicated their nearly simultaneous discovery of the Fundamental Theorem of Calculus-which links derivatives to integrals-in Latin anagrams! Jesus!
*****Nir Eyal is the most prominent writer I know of on behavioural design and habit in products. And he’s a great guy!
The featured image is from the Archimedes Palimpsest, one of the most exciting and beautiful books in the world. It is a Byzantine prayerbook-or euchologion-written on a piece of parchment paper that originally contained mathematical treatises by the Greek mathematician Archimedes. A palimpsest, for reference, is a manuscript or piece of writing material on which the original writing has been effaced to make room for later writing but of which traces remain. As portions of Archimedes’ original Archimedes are very hard to read, researchers recently took the palimpsest to the Stanford Accelerator Laboratory and threw all sorts of particles at it really fast to see if they might shine light on hard-to-decipher passages. What they found had the potential to change our understanding of the history of math and the development of calculus!
